5 - ប្រព័ន្ធចំនួន (Number System)

review នព្វន្ត លេខ ចំនួន នព្វន្តមូលដ្ឋាន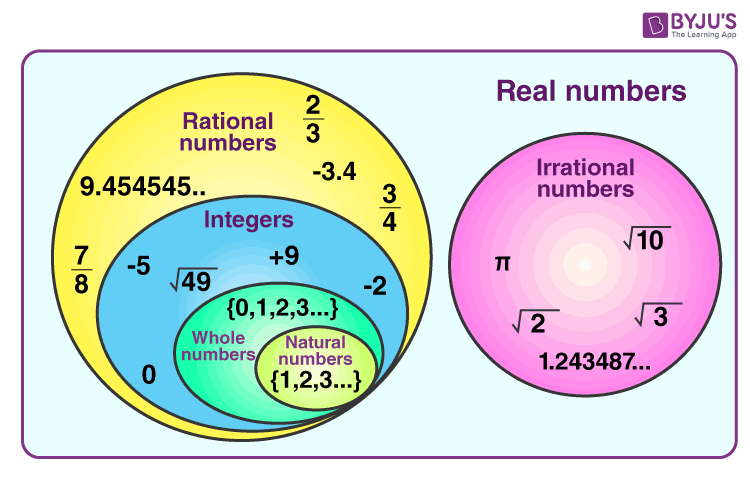

ប្រព័ន្ធចំនួន គឺជាគ្រឹះគ្រឹះនៃគណិតវិទ្យា ដែលជួយយើងរៀបចំ និងយល់ពីចំនួនផ្សេងៗគ្នាដែលយើងប្រើប្រាស់ក្នុងជីវិតប្រចាំថ្ងៃ និងក្នុងការដោះស្រាយបញ្ហាគណិតវិទ្យា។ យើងនឹងរៀនពីចំនួនប្រភេទសំខាន់ៗចំនួន ៥ ដូចខាងក្រោម៖

1. ចំនួនគត់ធម្មជាតិ (Natural Numbers)
2. ចំនួនគត់ (Integers) ឬ ចំនួនរឺឡាទីប (Relative Numbers)
3. ចំនួនសនិទាន (Rational Numbers)
4. ចំនួនអសនិទាន (Irrational Numbers)
5. ចំនួនកុំផ្លិច (Complex Numbers)

១. ចំនួនគត់ធម្មជាតិ (Natural Numbers)

• និមិត្តសញ្ញា: $\mathbb{N}$
• និយមន័យ: គឺជាចំនួនដែលយើងប្រើសម្រាប់រាប់វត្ថុ ឬមនុស្ស។ វាចាប់ផ្តើមពីលេខ $1$ ហើយបន្តទៅគ្មានទីបញ្ចប់។ ចាប់ផ្តើមពី​ $1$​ ឡើងទៅ ។
• ឧទាហរណ៍:
  • $1,2,3,4,5,\dots$
  • $10,20,100,\dots$

២. ចំនួនគត់ (Integers) ឬ ចំនួនរឺឡាទីប (Relative Numbers)

• និមិត្តសញ្ញា: $\mathbb{Z}$
• និយមន័យ: គឺជាសំណុំនៃចំនួនគត់ធម្មជាតិទាំងអស់ ចំនួនសូន្យ ($0$) និងចំនួនគត់អវិជ្ជមានទាំងអស់។
• ឧទាហរណ៍:
  • $\dots ,-3,-2,-1,0,1,2,3,\dots$
  • $-5$ (សីតុណ្ហភាព $-5^{\circ }C$)
  • $0$ (កម្ពស់សូន្យម៉ែត្រពីនីវ៉ូទឹកសមុទ្រ)
  • $15$ (ប្រាក់ចំណេញ $15$ ដុល្លារ)
• ហេតុផលដែលយើងត្រូវការវា: ដើម្បីតំណាងឱ្យតម្លៃដែលមានទិសដៅ ដូចជាបំណុល សីតុណ្ហភាពក្រោមសូន្យ កម្ពស់ក្រោមនីវ៉ូទឹកសមុទ្រ ឬការបាត់បង់។
• ទំនាក់ទំនង: ចំនួនគត់ធម្មជាតិ គឺជាផ្នែកមួយនៃចំនួនគត់។ ($\mathbb{N}\subset \mathbb{Z}$)

៣. ចំនួនសនិទាន (Rational Numbers)

• និមិត្តសញ្ញា: $\mathbb{D}$
• និយមន័យ: គឺជាចំនួនណាដែលអាចសរសេរជាប្រភាគ $\frac{a}{b}$ ដែល $a$ និង $b$ ជាចំនួនគត់ ហើយ $b$ មិនស្មើនឹងសូន្យ ($b\ne 0$) ។
  • វារួមបញ្ចូលទាំងប្រភាគ (ទាំងវិជ្ជមាន និងអវិជ្ជមាន) ទសភាគកាត់ផ្តាច់ (terminating decimals) និងទសភាគដដែលៗ (repeating decimals)។
• ឧទាហរណ៍:
  • ប្រភាគ: $\frac{1}{2},\frac{3}{4},-\frac{5}{7},\frac{10}{3}$
  • ទសភាគកាត់ផ្តាច់: $0.5$ (ព្រោះ $0.5=\frac{1}{2}$)
  • $2.75$ (ព្រោះ $2.75=\frac{275}{100}=\frac{11}{4}$)
  • $-3.125$ (ព្រោះ $-3.125=-\frac{3125}{1000}=-\frac{25}{8}$)
  • ទសភាគដដែលៗ: $0.333\dots$ (ព្រោះ $0.333\dots =\frac{1}{3}$)
  • $0.142857142857\dots$ (ព្រោះ $0.142857\dots =\frac{1}{7}$)
  • ចំនួនគត់: $5$ (ព្រោះ $5=\frac{5}{1}$)
  • $-2$ (ព្រោះ $-2=\frac{-2}{1}$)
• ហេតុផលដែលយើងត្រូវការវា: សម្រាប់តំណាងឱ្យផ្នែក ឬចំណែកនៃចំនួនគត់ ដូចជាការបែងចែកនំខេក គណនាការបញ្ចុះតម្លៃ ឬទំហំសម្លៀកបំពាក់។
• ទំនាក់ទំនង: ចំនួនគត់ គឺជាផ្នែកមួយនៃចំនួនសនិទាន។ ($\mathbb{Z}\subset \mathbb{D}$)

៤. ចំនួនអសនិទាន (Irrational Numbers)

• និមិត្តសញ្ញា: $\mathbb{Q}$
• និយមន័យ: គឺជាចំនួនដែល មិនអាច សរសេរជាប្រភាគ $\frac{a}{b}$ បានទេ។
• ឧទាហរណ៍:
  • ឫសការ៉េដែលមិនមែនជាចំនួនគត់: $\sqrt{2}\approx 1.41421356\dots$
  • $\sqrt{3}\approx 1.73205081\dots$
  • $\sqrt{5}\approx 2.23606798\dots$ *ចំនួនថេរល្បីៗ:
  • $\pi$ (P-i) : តំណាងឱ្យសមាមាត្ររវាងបរិមាត្រ និងអង្កត់ផ្ចិតនៃរង្វង់។ $\pi \approx 3.14159265\dots$
  • $e$ (Euler’s number) : ជាថេរគណិតវិទ្យាដ៏សំខាន់ក្នុងការលូតលាស់អិចស្ប៉ូណង់ស្យែល។ $e\approx 2.71828182\dots$
• ហេតុផលដែលយើងត្រូវការវា: សម្រាប់តំណាងឱ្យប្រវែង ឬតម្លៃជាក់លាក់ដែលមិនអាចបង្ហាញជាប្រភាគសាមញ្ញបាន។
• ទំនាក់ទំនង: ចំនួនអសនិទាន និងចំនួនសនិទាន មិនត្រួតស៊ីគ្នាទេ ប៉ុន្តែរួមគ្នាបង្កើតបានជា ចំនួនពិត (Real Numbers) ។

៥. ចំនួនពិត (Real Numbers)

• និមិត្តសញ្ញា: $\mathbb{R}$
• និយមន័យ: គឺជាសំណុំនៃចំនួនសនិទាន និងចំនួនអសនិទានទាំងអស់។ និយាយជារួម គឺជាចំនួនទាំងអស់ដែលយើងអាចតំណាងលើបន្ទាត់ចំនួន (Number Line) បាន។
• ឧទាហរណ៍: រាល់ឧទាហរណ៍ខាងលើ (ចំនួនគត់ធម្មជាតិ, ចំនួនគត់, ចំនួនសនិទាន, ចំនួនអសនិទាន) សុទ្ធតែជាចំនួនពិត។
• ទំនាក់ទំនង: $\mathbb{D}\cup \mathbb{Q}=\mathbb{R}$ (សនិទានរួមជាមួយអសនិទាន ស្មើនឹងចំនួនពិត)។
  • $\mathbb{N}\subset \mathbb{Z}\subset \mathbb{D}\subset \mathbb{R}$
  • $\mathbb{Q}\subset \mathbb{R}$

៦. ចំនួនកុំផ្លិច (Complex Numbers)

• និមិត្តសញ្ញា: $\mathbb{C}$
• និយមន័យ: គឺជាចំនួនដែលមានទម្រង់ $a+bi$ ដែល $a$ និង $b$ ជាចំនួនពិត (Real Numbers) ហើយ $i$ គឺជា ឯកតានិម្មិត (imaginary unit) ដែលកំណត់ដោយ $i^2=-1$ (ឬ $i=\sqrt{-1}$) ។
  • $a$ ត្រូវបានគេហៅថា ផ្នែកពិត (real part) ។
  • $b$ ត្រូវបានគេហៅថា ផ្នែកនិម្មិត (imaginary part) ។
• ឧទាហរណ៍:
  • $3+2i$
  • $5-i$
  • $7i$ (ព្រោះ $7i=0+7i$)
  • $4$ (ព្រោះ $4=4+0i$) - នេះបង្ហាញថាចំនួនពិតទាំងអស់គឺជាផ្នែកមួយនៃចំនួនកុំផ្លិច។
• ហេតុផលដែលយើងត្រូវការវា: ចំនួនកុំផ្លិចត្រូវបានបង្កើតឡើងដើម្បីដោះស្រាយបញ្ហាគណិតវិទ្យា ជាពិសេសសមីការដែលឫសការ៉េនៃចំនួនអវិជ្ជមានលេចឡើង (ឧទាហរណ៍ $x^2=-1$ គ្មានដំណោះស្រាយជាចំនួនពិតទេ តែមានដំណោះស្រាយជាចំនួនកុំផ្លិច $x=\pm i$)។ វាក៏ត្រូវបានប្រើយ៉ាងទូលំទូលាយនៅក្នុងវិទ្យាសាស្ត្រ វិស្វកម្ម (ដូចជាអគ្គិសនី) និងរូបវិទ្យា។
• ទំនាក់ទំនង: ចំនួនពិត គឺជាផ្នែកមួយនៃចំនួនកុំផ្លិច។ ($\mathbb{R}\subset \mathbb{C}$)